1. Take an eight by eight grid (with 64 squares).
2. Fill it randomly with digits 1 through 8.
3. Now start at any number on the left most column.
4. Move that many spaces down your grid (going up to the top of the next column if you run out of space).
5. Whatever number you land on, take that many steps down the grid, moving to the top of the next column if you run out of space, and continue.
6. Continue this procedure, until you run out of room on the whole grid.
7. Mark the last spot you landed on.
8. Start again with a new number on the left most column of your grid. Redo the whole procedure.
9. Try again, starting with yet another number on the left most column of the grid. And again. And again.
10. What happened?
I tried this cool little experiment, and to my amazement, at the end, I always landed on the same square (the three with the red check mark) no matter where I started on the most left column. Here is my grid:
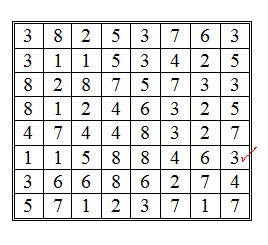
Of course the next question is: How does this work? Well if you look backwards at some of your moves, you must realize that if you hit the same spot at some point of the travel on the grid as in a previous attempt, then automatically you will get to the same final number. Therefore the probability of reaching one of those same spots along the way through the 64 spots is almost 100%. And so, every time you try going through the grid, you eventually hit the same spot, which will lead you to the same final number.
This is so interesting in several differnt ways. First of all, you choose random numbers – without a pattern. And what emerges is one determined spot. (Kind of like order emerging from chaos.) In fact if you tried to make a grid with a pattern, then you might not get to that one final spot everytime. For example, if I made a grid with all 8’s in all 64 spaces, our little experiment wouldn’t lead us to the same final spot every time. Isn’t that cool? It’s almost counter intuitive.
Another interesting phenomenon that comes out of this little experiment is that some of the numbers near the end of the grid are not visited by us at all. They could be changed, and it wouldn’t matter, we would still get to our final spot. The numbers that are landed are predetermined and nothing can change that. Even though the grid was initially arranged randomly, a kind of pattern forms from this “random” sequence.
We can look at this as a bit of a parallel with life: There is a random set of circumstances that we are given. This could be a set of genes, or the environmental conditions we were braught up in. That’s the grid. And then we choose a path, make decisions to lead our lives, to start from a given square at the beginning of our grid. But no matter which path we choose, our path is already predetermined, and we will end up in the same spot, no matter what we do initially. But maybe not. Maybe our life isn’t like that at all. Maybe our choices actually matter… who knows?!
Okay, I’m thinking about this cool little puzzle way too much. It’s math, not philosophy. But it’s cool anyway!

