In the recent movie: “21” a probability puzzle is presented:
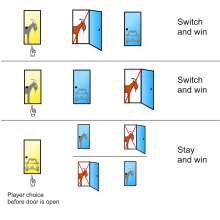
A quiz show contestant is lead to a room with three doors. Behind one of them there’s an expensive sports car; behind the other two there’s a goat. The candidate chooses one of the doors. But it is not opened; the host (who knows the location of the sports car) opens one of the other doors instead and shows a goat. The rules of the game, which are known to all participants, require the host to do this irrespective of the candidate’s initial choice. The candidate is now asked if he wants to stick with the door he chose originally or if he prefers to switch to the other remaining closed door. His goal is the sports car, of course!
The question now is:
* Is the candidate better off if he sticks with his original choice, * are his chances better if he switches, or * does it not matter whether he switches or not?
Some students came up to me and asked me about it in class the other day, and we had a fun discussion about it. Of course, I heard about the logic problem long before the movie came out. I heard about it in one of my logic classes back at university. I really should see that movie “21”.
Here is the solution and explanation in a nice little movie (I guess it’s called the Monty Hall Riddle):

