Recently I taught my son (grade 2) how to do subtraction of large numbers with borrowing. I am a high school math teacher, so I thought that teaching this subject would be a piece of cake. However, I didn’t realize that I would have to be this creative in order to actually get through to my son. Anyway, my method worked like a charm, so I’m posting it. It’s pretty basic, and I’m sure it has been widely used by good teachers (that really understand how to teach kids math), but in case you haven’t thought of this method, here it is.
(A) Prerequisites for the student:
1. Needs to know how to subtract simple numbers, or at least that subtraction means to “take away” objects.
2. Needs to know and understand the ones, tens, hundreds system of writing numbers (for example: if the number is 245, the student needs to know that this means there are 5 ones, 4 tens, and 2 hundreds).
(B) Method of Subtraction with borrowing:
1. In order for the child to understand what is subtraction, you can start with drawing circles or dots and then taking them away. For example you can write 7 – 2 =, and then underneath you would draw seven little circles. Then tell the child that “this is what you start with and now you have to subtract, or take away, two” (you can make up a story that you have seven candies and you ate two, or something simple like that). Anyway, then you proceed to erase two of the circles. (I use a white board, but a piece of paper will work if you use a pencil.) You ask: “How many are left?” The child then can count or just tell you how many. At the end you should fill in the number 5 right after the = sign. Make sure you bring the two representations together (the numbers and the circles should match, so the child can see it’s the same thing but represented differently).
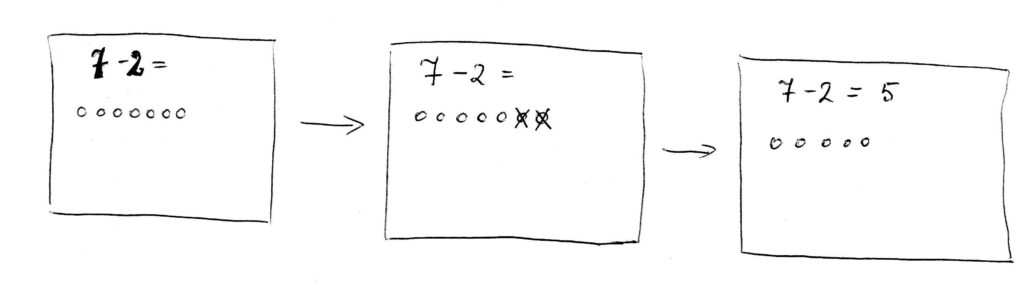
Repeat this until child feels really comfortable with the procedure of simple subtraction.
2. Then you continue with larger numbers, like two digit numbers and do the same procedure with the circles. For example, you write 35 – 14 =, and then draw (or have the child draw) 35 small circles. Make sure to make a big deal out of the fact that it takes a long time to draw these circles… that 35 is actually a big number. Then ask the child to “take away” (erase) 14. Ask how many there are left and write the number beside the = sign, just like before.
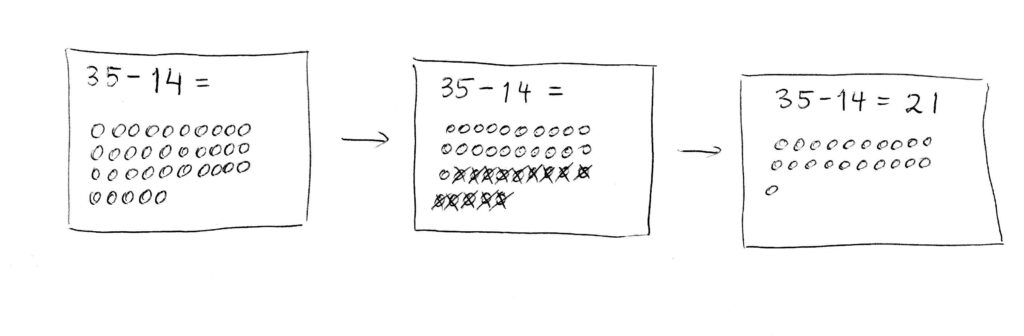
Make sure you leave this equation up – don’t erase it before the next step.
3. Now you are ready to introduce ones, tens, hundreds notation. For example, you can come back to your “complaining” how long it took to draw the 35 circles. Then tell your student that mathematicians are actually very lazy and they always look for ways to simplify things, make life easier for themselves. So instead of drawing 35 circles, mathematicians group circles in groups of 10. And for each group of ten circles mathematicians write a different symbol, like a line instead of a circle. So in our case there are 3 groups of 10 circles and 5 left behind. To do the simpler representation, we would draw 3 lines and five circles, instead of the 35 circles that we did at the beginning. You should practice this notation until the student feels really comfortable with the new notation (circle = ones, line = tens).
4. New notation and subtraction (no borrowing). Now, after your student understands the new notation and knows how to create any two digit number with sticks and circles, you should see if they can use it to subtract. Go back to your original example, 35 – 14 = . Tell the student to draw 35 with the new notation, and just as a reminder, somewhere on the side, ask them also to draw 14 in the new notation (with 4 circles and 1 line). Then ask them to take away 14 from the 35 they drew. If they don’t get it themselves, lead them to understand that they should be taking away 4 circles from the 5 circles and 1 line from the 3 lines (see picture below). So they don’t actually have to count 14 anymore, but 1 line and 4 circles. Write the answer after the = sign and point to your original example, showing that the answer is the same.
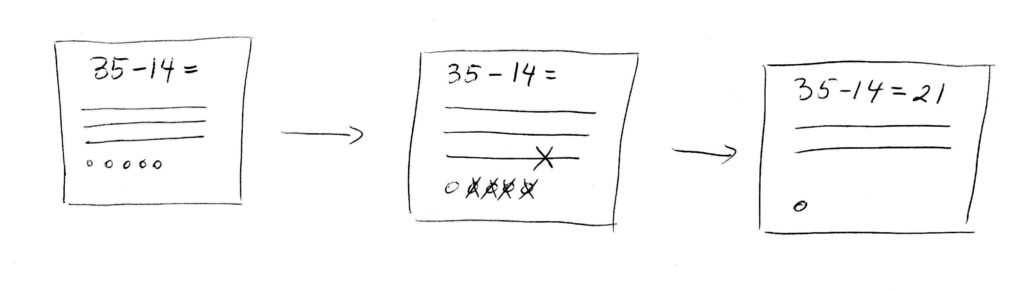
Make sure you emphasize that this is much simpler than first drawing 35 circles and then counting 14 circles to take away, like they did originally. Practice this with similar examples. Make sure there’s no “borrowing” involved at this stage. Just get them accustomed to this method.
5. New notation and subtraction with borrowing. After you feel the student is happy with this cool new method, give them a problem they can’t do: i.e. one that involves borrowing. For example: 35-17. Let them figure out on their own that this is not possible with the new notation… they should figure out that you cannot take away 7 circles from 5 circles. So then you say, what can we do? Let the kid think on it for a while. Don’t push, but eventually give them the solution: Remind them what each line represents. Say, “But doesn’t this line just mean there are 10 circles there? So can’t we redraw one of these lines as 10 circles?” And that’s what you do. You erase one of the lines and instead draw 10 more circles. Then ask your student to “take away” 7 from the 15 circles. This time it’s possible. And continue with the lines, taking away 1 line from the 2 that remained.
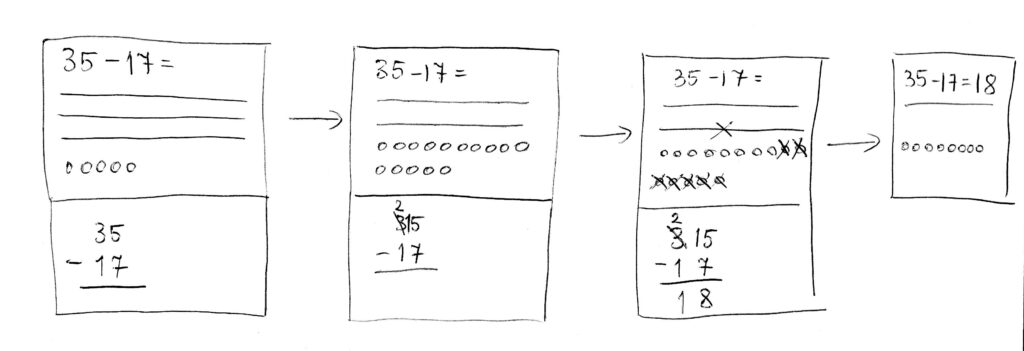
When doing the example, make sure you show how this can be done simply with the number representation (i.e. crossing out the 3, putting a 2 on top of the 3, and at the same time putting a 1 by the 5 – see diagram below). Make sure you always link the picture with the “math” representation.
6. You can extend this method to hundreds and three digit numbers easily. The symbol I used for hundreds was a square, because if you put 10 lines side by side, you’ll get a square sort of picture.
7. Finally: practice, practice, practice. Math, as you probably know, is all about practice. Let your students practice this subtraction. Let them use the circles and lines and squares initially, but tell them that they should get used to the easy way with numbers, because it’s actually much faster than drawing circles and lines and squares. But don’t scold them if they continue using the method for a while… they’ll learn to do the math problems without it soon enough.
Try it out and let me know how it works for you, or maybe you have your own methods…

